Have you ever wondered how a continuous line on a graph can suddenly “break,” or how a function can approach a specific value without ever actually reaching it? These concepts, central to calculus, are embodied in the study of limits and continuity. Understanding these core concepts is crucial for comprehending the behavior of functions and their applications in various fields, from physics and engineering to economics and finance.

Image: www.docsity.com
This comprehensive guide will delve into the world of limits and continuity, unraveling their complexities and showcasing the beauty of their applications. Prepare to embark on a journey that explores problems, provides solutions, and ultimately empowers you to grasp the fundamental principles of calculus.
The Essence of Limits: A Gateway to Continuity
Defining the Limit: A Function’s Approach
The concept of a limit hinges on the idea of a function’s behavior as its input value approaches a specific point. We say that a function f(x) has a limit L as x approaches “a” (written as lim x→a f(x) = L) if the output of the function gets arbitrarily close to L as x gets arbitrarily close to “a”, without actually reaching “a”. Think of it as a detective story where we’re trying to figure out what value the function is sneaking up on as its input gets closer and closer to a certain point.
Visualizing Limits: Graphing the Behavior
The essence of limits becomes clearer when visualized on a graph. Imagine a function whose graph seems to approach a particular point as x gets closer to a certain value. The limit at that point represents the value the function “wants” to achieve as x gets infinitely close, even if the function itself is not defined at that specific value.
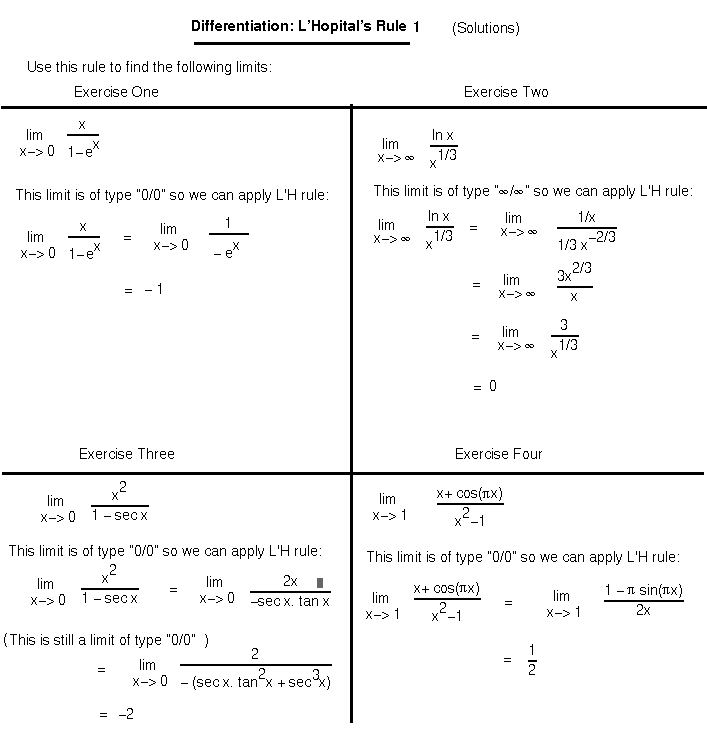
Image: gersgiasbwa.blogspot.com
Types of Limits: One-Sided and Two-Sided
There are two main types of limits:
- One-Sided Limits: These examine the behavior of the function as x approaches a certain value from either the left or the right side.
- Two-Sided Limits: These evaluate the function’s behavior as x approaches from both sides. For a two-sided limit to exist, both one-sided limits must exist and be equal.
Continuity: The Unveiling of Seamless Connections
Defining Continuity: A Function’s Graceful Flow
A function is considered continuous at a point “a” if three conditions are met:
- The function is defined at “a”.
- The limit of the function as x approaches “a” exists.
- The limit of the function as x approaches “a” is equal to the function’s value at “a”.
Essentially, a function is continuous at a point if its graph can be drawn without lifting your pen.
Types of Discontinuity: The Breaks in the Flow
When a function fails to meet the continuity criteria, we encounter a discontinuity. There are three primary types of discontinuity:
- Removable Discontinuity: The function has a hole at the point of discontinuity, but the limit exists and is finite.
- Jump Discontinuity: The function has a sudden jump in its value at the point of discontinuity.
- Infinite Discontinuity: The function approaches infinity (or negative infinity) at the point of discontinuity.
Problem-Solving Strategies: Navigating the Complexity
Using Direct Substitution: The Simplest Approach
When dealing with limits, the first thing to try is direct substitution. If substituting the value of “a” into the function produces a valid result, that result is the limit. This approach simplifies many problems.
Factoring and Simplifying: Unveiling the Hidden Limit
If direct substitution leads to an indeterminate form (like 0/0), factoring and simplifying the expression can often help. By canceling out common factors, the function may be transformed into a form where direct substitution becomes possible.
Rationalizing the Numerator or Denominator: Resolving Indetermination
When faced with limits involving radicals, rationalizing the numerator or denominator can be effective. By multiplying both the numerator and denominator by a suitable conjugate, the expression can be simplified, resolving the indeterminate form.
Applying L’Hôpital’s Rule: A Powerful Technique
For limits involving indeterminate forms like 0/0 or ∞/∞, L’Hôpital’s Rule can be a game-changer. This rule states that if the limit of the ratio of two functions is indeterminate, the limit is equal to the limit of the ratio of their derivatives (provided the latter limit exists).
Evaluating Limits at Infinity: Unveiling End Behavior
Limits at infinity help us understand the end behavior of functions as x approaches positive or negative infinity. Techniques like factoring out the highest power of x and dividing by dominant terms can be used to determine the limit.
Applications and Real-World Examples: Limits and Continuity in Action
Calculating the Instantaneous Rate of Change: Finding the Slope of a Tangent Line
Limits are fundamental to calculus’ concept of derivatives, which allows us to calculate the instantaneous rate of change of a function. This is essential in physics to find velocity and acceleration, or in economics to understand the rate of change of prices.
Modeling Continuous Processes: Representing Real-Life Phenomena
Continuity is vital in modeling real-world phenomena that exhibit smooth, continuous change. Examples include:
- Temperature Changes: The temperature of a room can be modeled as a continuous function of time, smoothly transitioning from one value to another.
- Population Growth: In a natural environment, population growth often follows a continuous model.
Optimizing Processes: Finding the Best Solution
Limits and continuity play a role in optimization problems, where we aim to find the maximum or minimum value of a function. By understanding the behavior of a function near its critical points (where the derivative equals zero or is undefined), we can optimize various processes in engineering, business, and other fields.
Limits And Continuity Problems With Solutions Pdf
Conclusion: A Foundation for Further Exploration
Understanding limits and continuity is a stepping stone into the realm of calculus. These core concepts provide a foundation for unraveling the complexities of functions, their derivatives, integrals, and countless applications. As you continue your journey in mathematics, remember the insights gained from exploring limits and continuity – they will serve as invaluable tools in your quest for deeper understanding.
So, don’t just stop here! Explore further resources, engage in problem-solving, and share your experiences. You’ll be amazed by the power and elegance of limits and continuity, and how they reshape our perception of the world around us.






