Have you ever noticed how train tracks seem to stretch into the distance, always maintaining the same distance apart? That’s a perfect example of parallel lines! And those crosswalks that form a perfect “T” at the intersection? Those are perpendicular lines. These concepts, seemingly simple, are fundamental to geometry and play a crucial role in understanding the world around us. In this unit, you’ll delve deeper into the fascinating world of parallel and perpendicular lines, unlocking their secrets and mastering their properties.
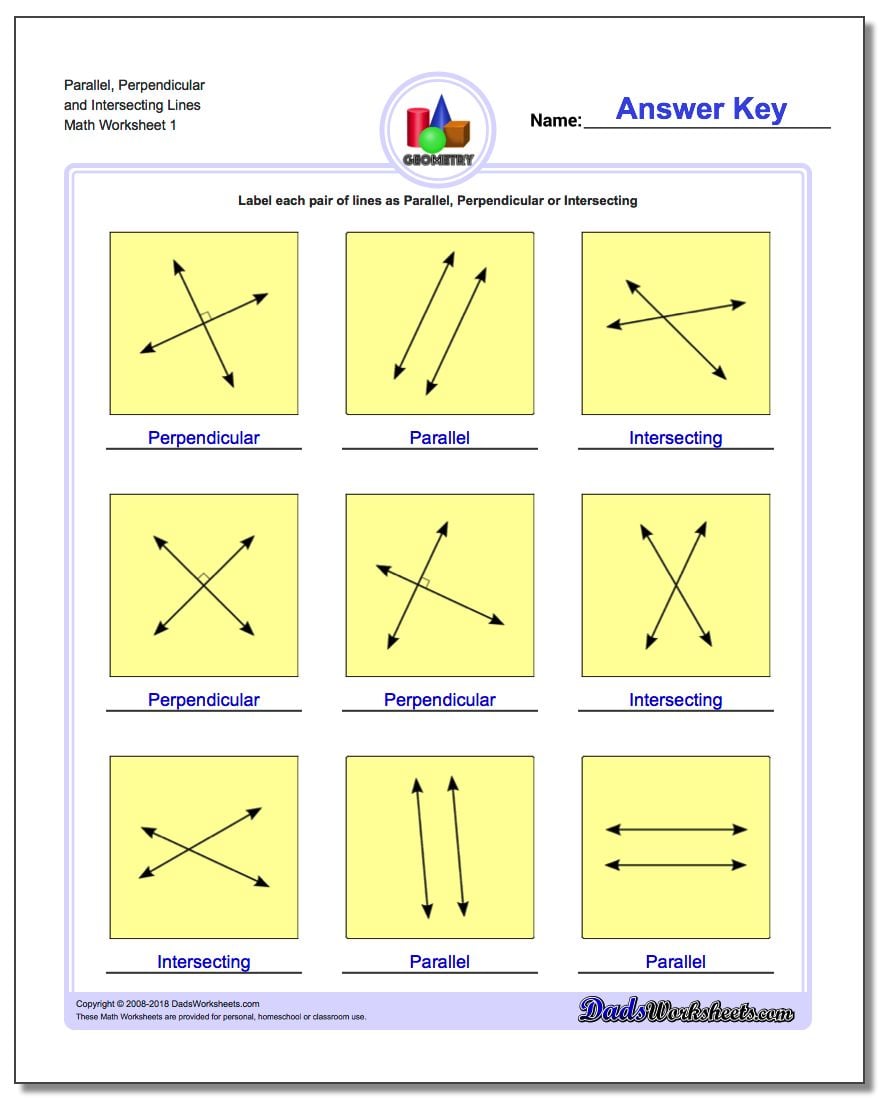
Image: www.dadsworksheets.com
This comprehensive study guide will equip you with the tools and knowledge to navigate this essential unit. We’ll explore the defining characteristics, relationships, and applications of parallel and perpendicular lines. Whether you’re a student preparing for an exam or simply curious about the beauty of geometry, this guide will serve as your reliable compass.
Parallel Lines: A Definition and Key Properties
Parallel lines are like two straight roads running side by side, never meeting, no matter how far they extend. Geometrically, two lines are considered parallel if they lie in the same plane and never intersect. This ‘never intersecting’ property is the defining characteristic of parallel lines.
For parallel lines, several important properties hold true. Firstly, parallel lines have the same slope. This is a crucial concept that allows us to determine if lines are parallel by simply comparing their slopes. Secondly, the corresponding angles formed by a transversal line crossing two parallel lines are equal. Similarly, alternate interior angles are equal, and same-side interior angles are supplementary (they add up to 180 degrees). These angle relationships provide a powerful tool for solving problems involving parallel lines.
Perpendicular Lines: The Perfect Right Angle
Perpendicular lines, on the other hand, are like the cross-bars in a ladder, intersecting at a precise 90-degree angle. This right angle is the defining feature of perpendicular lines. They represent the concept of ‘orthogonality,’ a fundamental idea in geometry and other mathematical fields.
One of the key properties of perpendicular lines is that their slopes are negative reciprocals of each other. This means that if one line has a slope of “m,” the perpendicular line’s slope will be “-1/m”. This relationship allows us to determine if two lines are perpendicular by examining their slopes. Moreover, the angles formed by two perpendicular lines are always right angles, making them essential for constructing squares, rectangles, and other geometric figures.
Understanding Slopes and their Role in Determining Parallelism and Perpendicularity
The slope of a line is a fundamental concept that helps us understand the direction and steepness of a line. It’s calculated as the “rise over run,” or the change in “y” divided by the change in “x” between any two points on the line.
The slope plays a crucial role in determining the relationships between lines. As previously mentioned, parallel lines have the same slope. This means if two lines have the same rise over run, they will maintain a constant distance and never intersect. Conversely, perpendicular lines have slopes that are negative reciprocals of each other. This means that one line’s slope is the inverse of the other, but with the opposite sign. This property ensures that the lines intersect at a right angle.
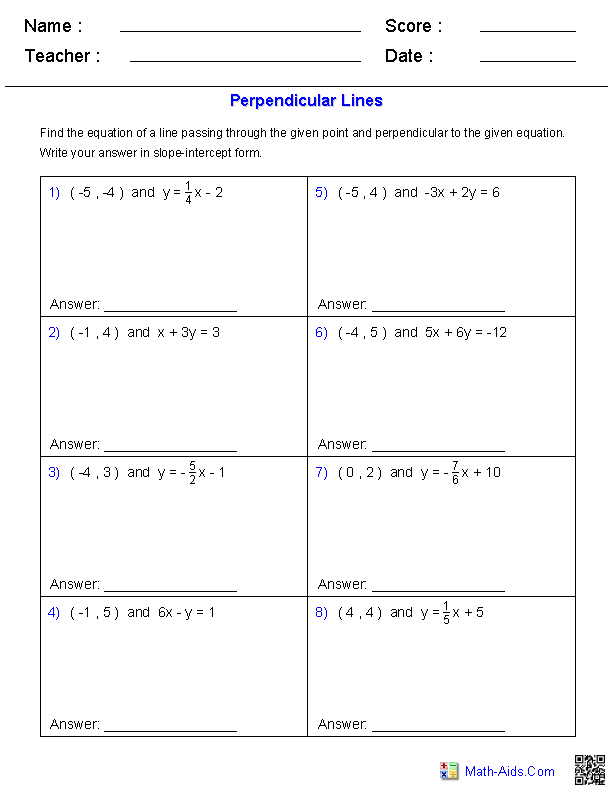
Image: goodimg.co
Applications of Parallel and Perpendicular Lines in Real Life
The concepts of parallel and perpendicular lines extend far beyond the realm of textbooks. They are fundamental to numerous real-world applications. Architects use these principles to design buildings and structures, ensuring stability and functionality. Engineers utilize them to construct bridges, roads, and other infrastructure, optimizing design and ensuring safety. Even in everyday life, parallel and perpendicular lines are evident in our surroundings, from the rectangular grids of city streets to the parallel rails of roller coasters.
The importance of these concepts is particularly evident in the field of carpentry and construction. Carpenters rely on parallel and perpendicular lines to ensure precise alignment and stability in structures. For instance, they utilize a level to ensure that walls and floors are parallel, preventing unevenness and potential structural issues. Similarly, they employ squares to guarantee that beams and other components are perpendicular to each other, contributing to the strength and integrity of the built environment.
Tips for Success: Master Parallel and Perpendicular Lines in Unit 3
Mastering the concepts of parallel and perpendicular lines requires not only understanding the definitions and properties but also sharpening your problem-solving skills. Here are some tips to help you excel in this unit:
- Visualize the Concepts: Draw diagrams and label components to gain a deeper understanding of the relationships between lines and angles.
- Practice, Practice, Practice: Solve numerous problems related to parallel and perpendicular lines. The more you practice, the better your understanding will be.
- Seek Help When Needed: Don’t hesitate to ask your teacher or classmates for clarification if you encounter difficulties. Working together can enhance your comprehension.
- Connect with Real-World Applications: Look for examples of parallel and perpendicular lines in your surroundings. This connection will help you visualize and understand the concepts in a practical context.
By following these tips, you’ll build a strong foundation in parallel and perpendicular lines. Remember, understanding these concepts is vital for your overall success in geometry and other areas of mathematics. The effort you put in now will pay off in the long run.
Frequently Asked Questions (FAQs)
What is the difference between parallel and perpendicular lines?
Parallel lines never intersect, while perpendicular lines intersect at a right angle (90 degrees). This difference is reflected in their slopes: Parallel lines have the same slope, whereas perpendicular lines have slopes that are negative reciprocals of each other.
How do I identify parallel lines?
Two lines are parallel if they have the same slope. Alternatively, parallel lines can be identified using the angle relationships formed by a transversal line: corresponding angles are equal, alternate interior angles are equal, and same-side interior angles are supplementary.
How do I identify perpendicular lines?
Two lines are perpendicular if their slopes are negative reciprocals of each other. Alternatively, you can identify perpendicular lines by looking for a right angle (90 degrees) at their point of intersection.
What are some real-world examples of parallel and perpendicular lines?
Examples abound in our daily lives: train tracks are parallel, a ladder leaning against a wall is perpendicular, and the intersecting grid of city streets forms numerous examples of both parallel and perpendicular lines.
Unit 3 Study Guide Parallel And Perpendicular Lines
Conclusion
Unit 3’s exploration of parallel and perpendicular lines introduces fundamental concepts that extend beyond geometry into various scientific and engineering fields. Understanding their properties, relationships, and applications is crucial for mastering geometric principles and applying them to real-world problems.
Are you ready to delve deeper into the intriguing world of parallel and perpendicular lines? If you’re eager to explore more, discover valuable resources online and engage in discussions with fellow learners. The journey of mathematical discovery is always rewarding!






