Have you ever found yourself staring at a right triangle, feeling lost in a sea of sine, cosine, and tangent? I remember the first time I encountered trigonometry in high school. It felt like a foreign language, filled with confusing ratios and obscure formulas. But, as I delved deeper, I realized the beauty and power behind right triangle trigonometry. It’s not just about memorizing formulas; it’s about understanding the relationships between angles and sides, which unlocks a world of problem-solving capabilities.
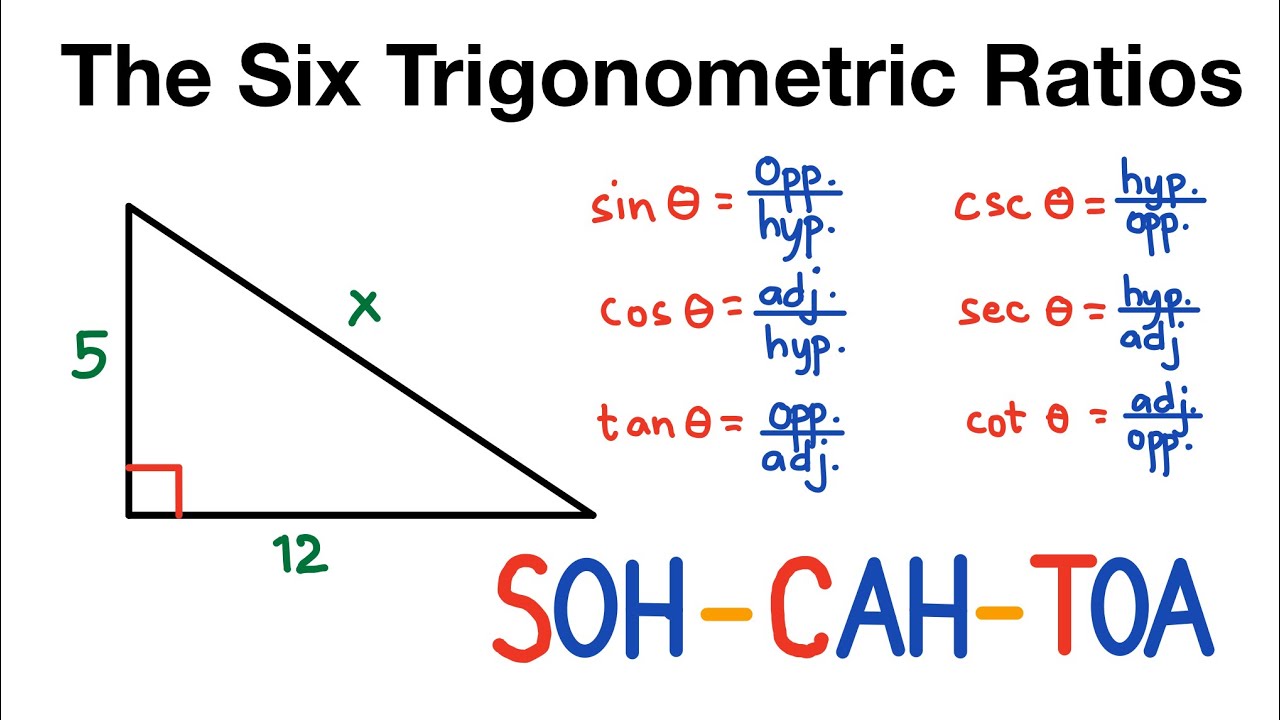
Image: www.youtube.com
Today, we’ll embark on a journey to understand the fundamentals of right triangle trig, specifically focusing on evaluating trigonometric ratios. We’ll demystify the process, revealing the logic and practical application of these concepts. So, grab your calculator and let’s explore the world of triangles!
Understanding the Basics: Defining Trig Ratios
Before we dive into evaluating ratios, let’s clarify the fundamental definitions. In a right triangle, the three primary trigonometric ratios – sine (sin), cosine (cos), and tangent (tan) – are defined in relation to the angles and the sides of the triangle:
Defining Sine, Cosine, and Tangent
- Sine (sin): The sine of an angle is the ratio of the length of the side opposite the angle to the length of the hypotenuse.
- Cosine (cos): The cosine of an angle is the ratio of the length of the side adjacent to the angle to the length of the hypotenuse.
- Tangent (tan): The tangent of an angle is the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle.
Remember the acronym SOH CAH TOA, which can be a handy mnemonic for recalling these definitions:
SOH CAH TOA:
Sine = Opposite / Hypotenuse
Cosine = Adjacent / Hypotenuse
Tangent = Opposite / Adjacent
Here’s an example:
| Angle | Opposite | Adjacent | Hypotenuse | sin | cos | tan |
|---|---|---|---|---|---|---|
| A | 3 | 4 | 5 | 3/5 | 4/5 | 3/4 |
| B | 4 | 3 | 5 | 4/5 | 3/5 | 4/3 |
Evaluating Trig Ratios: A Step-by-Step Guide
Now that we’ve established the fundamental definitions, let’s delve into the practical process of evaluating trigonometric ratios. Here’s a step-by-step guide:

Image: www.coursehero.com
Steps for Evaluating Trig Ratios
- Identify the Right Angle: Locate the right angle in the triangle. This will help you identify the hypotenuse.
- Identify the Angle of Interest: Determine which angle you are evaluating the trig ratio for.
- Label the Sides: Label the sides of the triangle as “opposite,” “adjacent,” and “hypotenuse” in relation to the angle of interest.
- Determine the Trig Ratio: Decide whether you need to calculate sine, cosine, or tangent based on the given information.
- Apply the Formula: Utilize the appropriate formula (SOH CAH TOA) to calculate the ratio.
- Simplify: If possible, simplify the fraction to its simplest form.
Examples of Trig Ratio Evaluations
Let’s solidify the process by working through a few examples:
Example 1: Finding sin(A)
Given a right triangle with sides of 3, 4, and 5, where angle A is the angle of interest, calculate sin(A).
Following the steps above, we can easily find that sin(A) = 3/5.
Example 2: Finding cos(B)
Given a right triangle with sides of 8, 15, and 17, where angle B is the angle of interest, calculate cos(B).
We can see that cos(B) = 15/17.
Example 3: Finding tan(C)
Given a right triangle with sides of 5, 12, and 13, where angle C is the angle of interest, calculate tan(C).
The tangent of angle C is tan(C) = 12/5.
The Power of Trig Ratios: Real-World Applications
Right triangle trigonometry is not just a theoretical concept; it has countless real-world applications! Imagine you’re trying to determine the height of a tall building using only a measuring tape and your knowledge of trigonometry. By measuring the angle of elevation and the distance from the building, you can use trig ratios to calculate the building’s height. This is just one simple example of how trigonometry plays a crucial role in fields like:
- Architecture: Designing structures, calculating angles, and ensuring stability.
- Engineering: Analyzing forces, building bridges, and constructing roads.
- Navigation: Calculating distances, determining directions, and charting courses.
- Physics: Modeling projectile motion, understanding wave phenomena, and analyzing oscillatory systems.
- Astronomy: Tracking celestial bodies, calculating distances, and studying the universe.
Expert Tips and Advice for Mastering Trig Ratios
Now that you have a solid understanding of the fundamentals, let’s delve into some expert tips to enhance your mastery of evaluating trig ratios:
Tips for Success in Trig
- Memorize SOH CAH TOA: This mnemonic is a powerful tool for remembering the definitions of sine, cosine, and tangent.
- Practice Regularly: Solving practice problems is crucial for solidifying your understanding and building confidence.
- Visualize the Triangle: Draw and label diagrams to aid your understanding of the relationships between angles and sides.
- Use Your Calculator: Learn to use your calculator efficiently to find the sine, cosine, and tangent of angles.
- Don’t Be Afraid to Ask for Help: If you’re struggling with a concept, reach out to your teacher or a tutor for guidance.
Remember, understanding the fundamentals is key to mastering any subject. By applying these tips and practicing diligently, you’ll find evaluating trig ratios to be a simpler and more enjoyable task.
Frequently Asked Questions
Q: Can I use the same trig ratios for different angles in the same triangle?
Yes, absolutely! The trig ratios for different angles in the same triangle will be different because they are based on the relationships between the sides and the specific angle you’re evaluating. So, sin(A) will not be the same as sin(B) in the same triangle.
Q: What happens if I don’t have all three sides of the triangle?
Don’t worry! You can still use trig ratios even if you only know two sides. By applying the Pythagorean theorem or using the given information to calculate the missing side, you can then evaluate the trig ratios for the desired angle.
Q: Why is the hypotenuse always involved in sine and cosine?
The hypotenuse represents the longest side of a right triangle and is crucial for relating the lengths of the other sides to the angles. The sine and cosine ratios utilize the hypotenuse to establish those relationships, which makes them essential for calculating angles and sides in right triangles.
Right Triangle Trig Evaluating Trig Ratios
https://youtube.com/watch?v=3rdTIwfEE1w
Conclusion
Right triangle trig, particularly evaluating trigonometric ratios, is a fundamental concept with wide-ranging applications in science, engineering, and everyday life. By understanding the definitions of sine, cosine, and tangent and mastering the step-by-step process for evaluating ratios, you’ll unlock the potential of trigonometry to solve complex problems and explore fascinating real-world scenarios. Remember, practice makes perfect! So, grab your calculator, explore right triangles, and discover the power of trigonometry!
Are you ready to dive deeper into right triangle trigonometry? What are some of your favorite applications of trigonometry? Share your thoughts in the comments below!






